
|
| Home | Downloads | Screenshots | Forums | Source code | RSS | Donate |
| Register | Log in |
| < A tour through melonDS's JIT recompiler Part 1Merry Christmas from the melonDS team! > |
|
Back in business Dec 10th 2020, by Arisotura |
|
Sometimes, there's nothing quite like an interesting issue to motivate a lazy Arisotura. For example: no graphics in the third flying level in Power Rangers - Super Legends. Basically:   Yeah, it's not very playable like this, even moreso as this is a shoot-em-up level. When I looked at this, I saw Generic was already on it. He figured out that, when entering the level, the horizontal offset for BG0 was not being reset, and its previous value was 256, which caused BG0 (and thus the 3D graphics) to be pushed offscreen. Moreover, NO$GBA and DeSmuME both suffered from the same issue, which meant that once again we were stepping into uncharted territory. Exciting! So I set to work. I logged what the game was doing and made a disassembly. There were two main possibilities there: either the game was misbehaving due to some emulation issue, or it was working as intended but relied on unknown hardware behavior. The second hypothesis seemed more likely, seeing as when entering the glitched level, the game took care to clear VRAM and setup 2D layers and all that. It didn't seem to be a timing issue either, as those are typically affected when tweaking melonDS's cache timing constants, but tweaking these made no change there. So, looking at my logs, I made several tests on hardware. I figured something was resetting the BG0 scroll position, but couldn't manage to reproduce that. So, seeing as it was 5:00, I went to bed, like normal people do. The next day, Generic gave me a test ROM that reproduced the issue at hand. It was one of the basic libnds 3D examples, except it was modified to write a value to BG0HOFS at the very beginning of main(), before doing anything else. Sure enough, the example cube found itself scrolled on melonDS, but not on hardware. Well, looks like after hours of banging our heads at that issue, he'd figured out something. Going from this, I was able to pinpoint the exact conditions that caused the BG0 scroll position to be reset. In particular, in the glInit() function: powerOn(POWER_3D_CORE | POWER_MATRIX); // enable 3D core & geometry engine
POWCNT1. I'd suspected it, I'd tried messing with it, but didn't find anything, because the hardware behavior was not what I'd expected. Basically, POWCNT1 is the ARM9-side power control register. It lets you enable or disable the 2D renderers, the two components of the 3D renderer (the geometry engine and the rendering engine), the screens, and also swap the screens. Fun shit. Further experiment showed us that, unlike what we thought, horizontal scrolling for the 3D layer isn't done by the 2D engine, but by the 3D rendering engine, right before the 3D layer is passed to the 2D engine. This was further confirmed by Hydr8gon, who observed that when capturing the 3D layer alone, it also has the scrolling applied. So how does this work? The 3D rendering engine has its own scroll position register, which is updated when writing to BG0HOFS. Except when the 3D rendering engine is disabled, in which case its register stays untouched. There we go. Sure enough, Power Rangers doesn't turn on the 3D renderer until it actually has to render 3D graphics, that is, in our glitched level. Hence, the scroll position given to BG0 in the previous 2D-only levels would never end up into the 3D rendering engine's scroll register. Sure enough, implementing that behavior into melonDS did the trick: 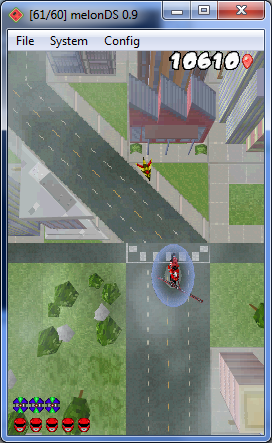 Did we tell you the DS has quirky hardware? |
| 10 comments have been posted. |
| < A tour through melonDS's JIT recompiler Part 1Merry Christmas from the melonDS team! > |
|
Generic aka RSDuck says: Dec 10th 2020 |
|
once again screwing around wins against the analytical approach :P While figuring out why BG0 is scrolled, I encountered another issue. For some reason there was no 3D at all because the color of the light was set to black. But it turned out that this was only an issue because light color wasn't included in savestates, so everytime I would load the savestate I made for quick testing, the default value would still be in there instead of what the game set it to earlier. We didn't notice this earlier because usually games would setup the light colors every frame. |
|
Laka says: Dec 11th 2020 |
| I really like seeing these technical posts, awesome job, as always! =) |
|
Masky says: Dec 11th 2020 |
| Watching this emulator’s progress is more exciting than any tv show on right now lol |
|
Anon says: Dec 13th 2020 |
|
^What Masky said! Honestly with every new post it seems like I underestimated my DS more and more. I never thought it'd be so complicated and cool. Then again respecting your DS when the only game you had for it was Rabbids for 10 years is kinda hard. I think these technical posts are gonna be really important for future devs who want to emulate some really out of the way software, or even just get into emulation in general. Keep up the good work, guys! |
|
Rayyan says: Dec 13th 2020 |
| Nice to see melonDS is making more firsts! |
|
Comlud says: Dec 24th 2020 |
| Merry Christmas! |
|
StLouisCPhT says: Dec 24th 2020 |
| Quirky hardware seems to be Nintendo's forte. |
|
Sorer says: Dec 24th 2020 |
| Sony got more quirky hardware tbh lol. |
|
Generic aka RSDuck says: Dec 25th 2020 |
| that really depends. There's no definitive answer to this, but e.g. the PS1 was definitely simpler than it's contemporaries the Saturn or the N64. |
|
ChainSwordCS says: Dec 31st 2020 |
| These posts detailing emulating quirks of hardware are super interesting, reminds me of a blog by Shonumi called Edge of Emulation. Those posts are great reads too. I love reading write-ups like this. |